更新日から1年以上経過しています。情報が古い可能性がございます。
社内勉強会としてPythonを教える機会があったので、
そこでのネタを公開。
ネタとしては、モンテカルロ法で円周率の算出をしてみようという話。
使用バージョンは以下の通り
・PYthon 3.6.2
・numpy 1.13.1
・pandas 0.20.3
算出の前に
知らない人のためにちょっと解説。
モンテカルロ法は乱数を用いたシミュレーション方法です。
厳密解を求めるのが難しい時に、乱数をたくさん用いて近似解を得ようというもの。
今回はPythonを用いているので、forループを用いた書き方と、
numpyを用いた書き方の2通りで書いて速度の比較もしてみます。
まずは必要なモジュールをインポートします。
Jupyterの上の方のセルに以下のコードを入力しておきます。
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
%matplotlib inline
plt.rcParams['figure.figsize'] = (10, 10)
ではさくさく進んでいきましょう。
forループを用いた方法
%%time
x = np.arange(0, 1.01, 0.01)
y = np.sqrt(1 - x ** 2)
plt.plot(x, y, c='g')
plt.xlim(0,1)
plt.ylim(0,1)
# モンテカルロ法による円周率の導出
c = 0
n = 1000
for i in range(0, n):
x = np.random.rand()
y = np.random.rand()
if x ** 2 + y ** 2 <= 1:
plt.scatter(x, y, c='b')
c += 1
else:
plt.scatter(x, y, c='r')
print('count: {0}, Π = {1}'.format(c, float(c) / n * 4))
実行結果として、以下の数値が出力されました。
count: 777, Π = 3.108
Wall time: 2.37 s
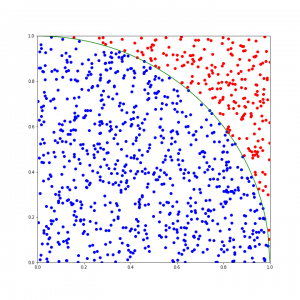
1000ループで円周率3.108と、比較的それっぽい数値が得られていますね。
しかし、実行に2.37秒と、大分遅いのが分かると思います。
これは、Jupyterのセルに%%timeと書いておくと、
そのセルの実行時間が表示されるので、それを用いています。
numpyを用いた方法
%%time
x = np.arange(0, 1.01, 0.01)
y = np.sqrt(1 - x ** 2)
plt.plot(x, y, c='g')
plt.xlim(0,1)
plt.ylim(0,1)
# モンテカルロ法による円周率の導出
n = 10_000
x = np.random.rand(n)
y = np.random.rand(n)
cond = x ** 2 + y ** 2 <= 1
c = len(x[cond])
plt.scatter(x[~cond], y[~cond], c='r')
plt.scatter(x[cond], y[cond], c='b')
print('count: {0}, Π = {1}'.format(c, float(c) / n * 4))
実行結果は以下。
count: 7853, Π = 3.1412
Wall time: 224 ms
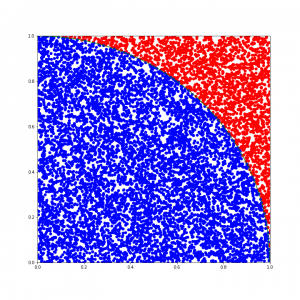
こちらは10,000個の点をプロットして算出しています。
円周率3.1412と、1,000ループよりも近い値が得られていますね。
また、ループに対して10倍の点をプロットしているにも関わらず、
処理時間が224 msと大分速くなっています。
numpyを使おう
Pythonのループは遅いです。
Cとかだとコンパイラが良しなに最適化してくれますが、
スクリプト言語だとそうは行きませんからね。
なので、numpyでまとめて乱数を生成して、
ループを使わずまとめてプロットすることでかなりの高速化が図れます。
と言うわけで、みんなもnumpyに親しもう!
補足
print分で4倍しているのは、1/4円しか利用していないからです。
4倍することで円で行うのと同等にしています。
あと、Pythonの乱数はメルセンヌ・ツイスタと言うアルゴリズムが用いられているので、
乱数の質が良いです。
Cとかだと線形合同法が使われていますが、この辺もその内実装して比較してみたいですね。